What Eta Squared can tell us
Imagine a study, where students have to nominate the highest and lowest achiever from their class in mathematics — up to three names, including themselves. The rationale about such a question would be to investigate the salience of same-gender role models as a function of different experimential conditions.
In your study, you would divide classes into same-gender groups and mixed-gender groups to investigate, whether this might have an impact on the nominations. You would collect some data and find that girls in the same-gender condition nominate 1.42 (SE = .24) high-math-ability girls, and in the mixed-gender condition 0.36 (SE = .23) girls. This result has been indeed found in a study by Huguet and Régner (2007, page 554).
What do you think, would be the explained variance (
To help you, let’s visualize the data in a common, but infamous plot, the so called “dynamite plot”:
library(lsr)
library(yarrr)
library(DescTools)
library(dplyr)
library(tidyr)
library(ggplot2)
library(kableExtra)
library(gganimate)
library(treemapify)#devtools::install_github("wilkox/treemapify")dynamite <- data.frame(group = c("mixed","same"), mean = c(1.42, 0.36), SE = c(.24, .23))
ggplot(dynamite, aes(x = group, y = mean, fill = group)) +
geom_bar(position = position_dodge(), stat = "identity") +
scale_fill_manual(values = c("#4D4D4D","#B3B3B3")) +
geom_errorbar(aes(ymin = mean-SE, ymax = mean+SE), width=.2, size = 1.1, position = position_dodge(.9)) +
ylab("Nominations")+
theme_bw() +
guides(fill = FALSE)+
theme(axis.text = element_text(size = 20)) +
theme(axis.title = element_text(size = 20))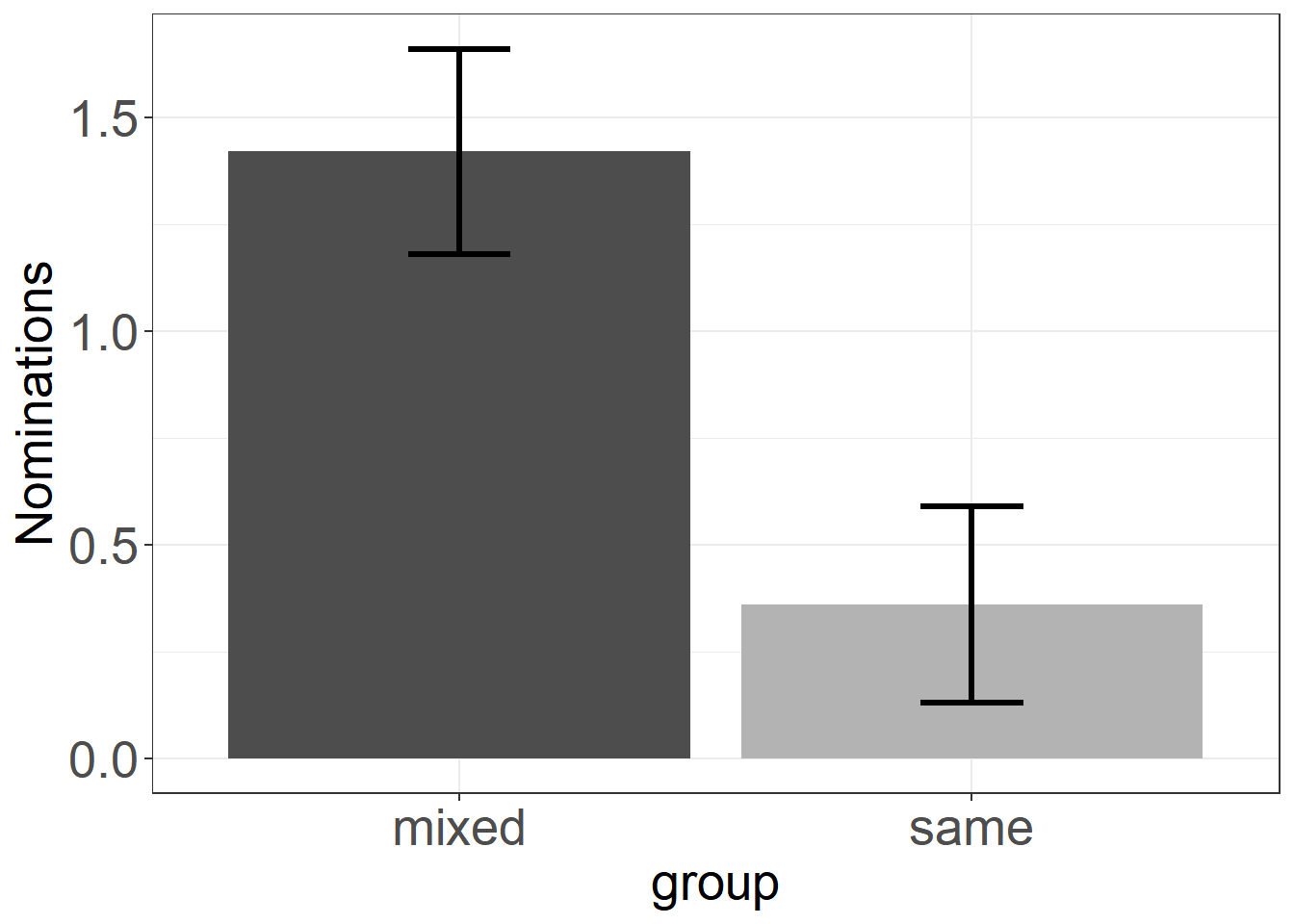
We see that the groups seem to differ quite a lot, but we do not see anything else than we already knew from the statistics of the mean and standard error above. Still, such plots are widely used in academia, even though their information can be displayed in a table with two rows (means and standard errors). A Hint: Do not use such plots, and try to ban them from papers you are writing or reviewing (see this post).
Now enough suspension, to unravel the magnitude of explained variance. Huguet & Régner (2007) reported the following result for their ANOVA:
F(1,216) = 8.92, p < .003,
So, the experimental condition explains a mere 4% of the variance in the data. If this value of
set.seed(2616)
n <- 218/2 # assuming, both experimental groups are equally large
mixed <- rnorm(n, mean = 1.42, sd = sqrt(n)*.24) #simulate sample from a normal distribution with the respective mean and standard deviation
same <- rnorm(n, mean = .36, sd = sqrt(n)*.23)
dt <- data.frame(group =c("mixed","same"), Mean=c(mean(mixed), mean(same)), Standard_Error =c(MeanSE(mixed), MeanSE(same)))
dt %>%
kable()%>%
kable_styling()| group | Mean | Standard_Error |
|---|---|---|
| mixed | 1.4225076 | 0.2553378 |
| same | 0.3614901 | 0.2208642 |
This adequately resembles the mean structure that we want to see. What does this data look like? Let’s use pirateplots from the yarrr-package, as a much better alternative to dynamite plots:
df <- data.frame(group=c(rep("mixed",n),rep("same",n)), value=c(mixed, same))
pirateplot(value ~ group, data=df, cex.lab=1.6)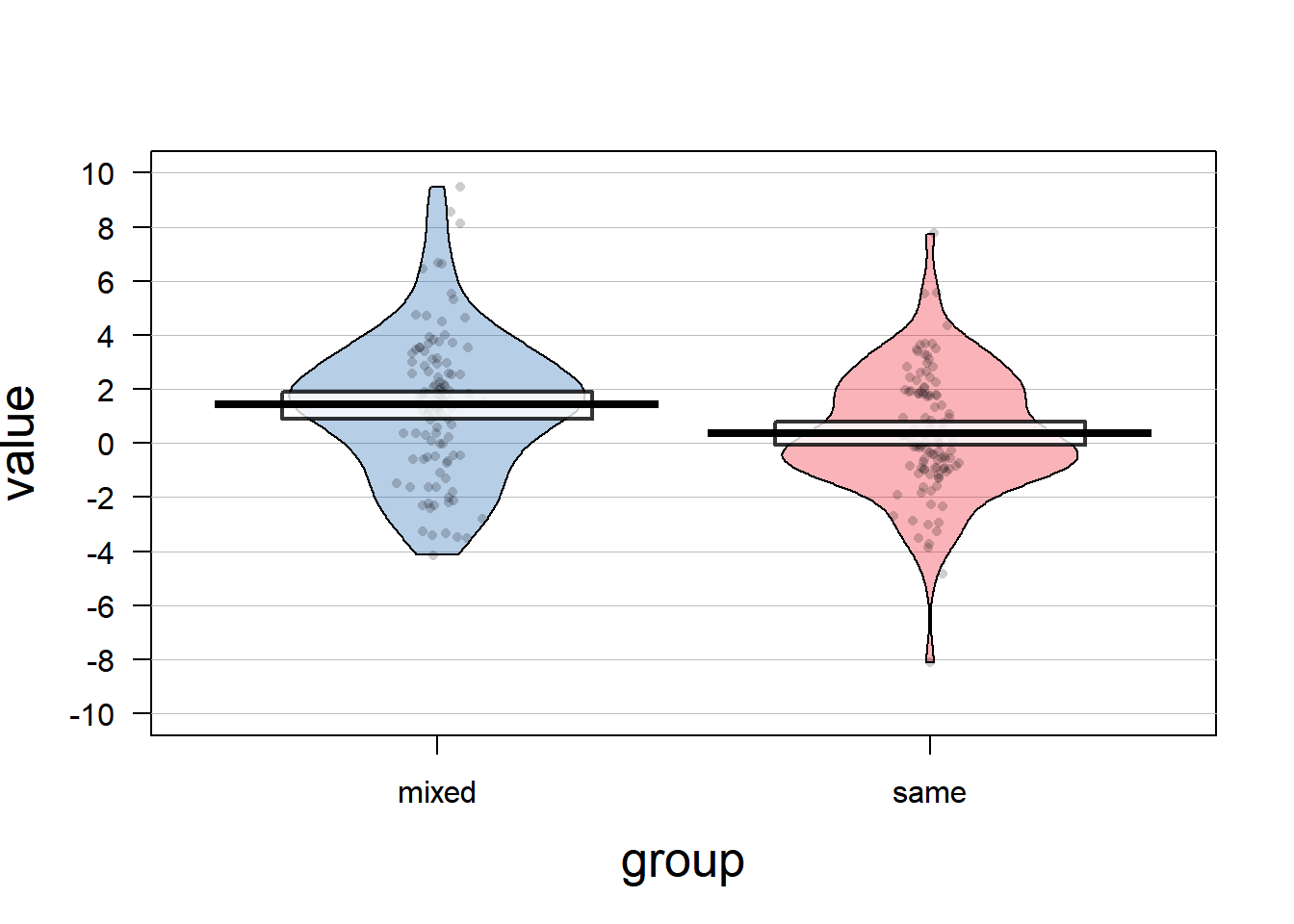
Interestingly, the data is scattered stronger than one might think when only looking at the mean and standard error reported in the study (regard the scale of the plot!). It is not a perfect simulation of the data that was used in the original article, because negative nominations are not possible. That might indicate, that the authors did not use the appropriate distribution and should have used the Poisson distribution for count data instead. However, for the sake of simplicity, we will stick with using normally distributed data.
May the small
mod1 <- aov(df$value ~df$group)
summary(mod1)
etaSquared(mod1)
Our F-value is even a little larger, and
Let’s look, at how else we could describe this data. As it is only two groups, Cohen’s d is also a possible measure for the effect size:
CohenD(mixed, same)## [1] 0.4257092
## attr(,"magnitude")
## [1] "small"A Cohen’s d around .4 can be considered small to medium (according to old conventions, but see this conference presentation), and I would admit that this looks better than an explained variation of 4%. What would it look as a correlation?
cor(df$value, as.numeric(df$group)) ## [1] -0.2091103Squaring this term would exactly lead to our eta-coefficient: r2=0.0437271.
This will only be true in the case that the independent variable consists of two groups. When there are more than two groups, then the two measures will only be equal, if the relationship between the variables is a linear one. If there is a non-linear relationship, then the difference between
How could we visualize the explained variance?
Visualizing variance, and even more so explained variance, is a tough attempt. A very nice visualization of explained variance was developed by W.J. Schneider here, but unfortunately it does not cover the explained variance in an ANOVA example. Thus, I started with an own visualization of the data that we already have so far.
df <- df %>%
# group_by(group) %>% # actually, we do not need the within variance, but total variance
mutate(grandmean = mean(value)) %>%
mutate(diff = value - grandmean) %>%
group_by(group) %>%
mutate(groupmean = mean(value)) %>%
ungroup()
pd = position_dodge(.01)
ggplot(df, aes(x=0, y=value, col=group))+
geom_point(alpha=.3, pos=pd, size=1.7)+
geom_hline(size=1.1, aes(yintercept=grandmean), linetype="dashed")+
xlim(-.2,9)+
coord_fixed()+
theme_bw()+
geom_text(aes(x=7.3, y=0.6), label="Grand Mean",size=3.8, col="black",
fontface="bold")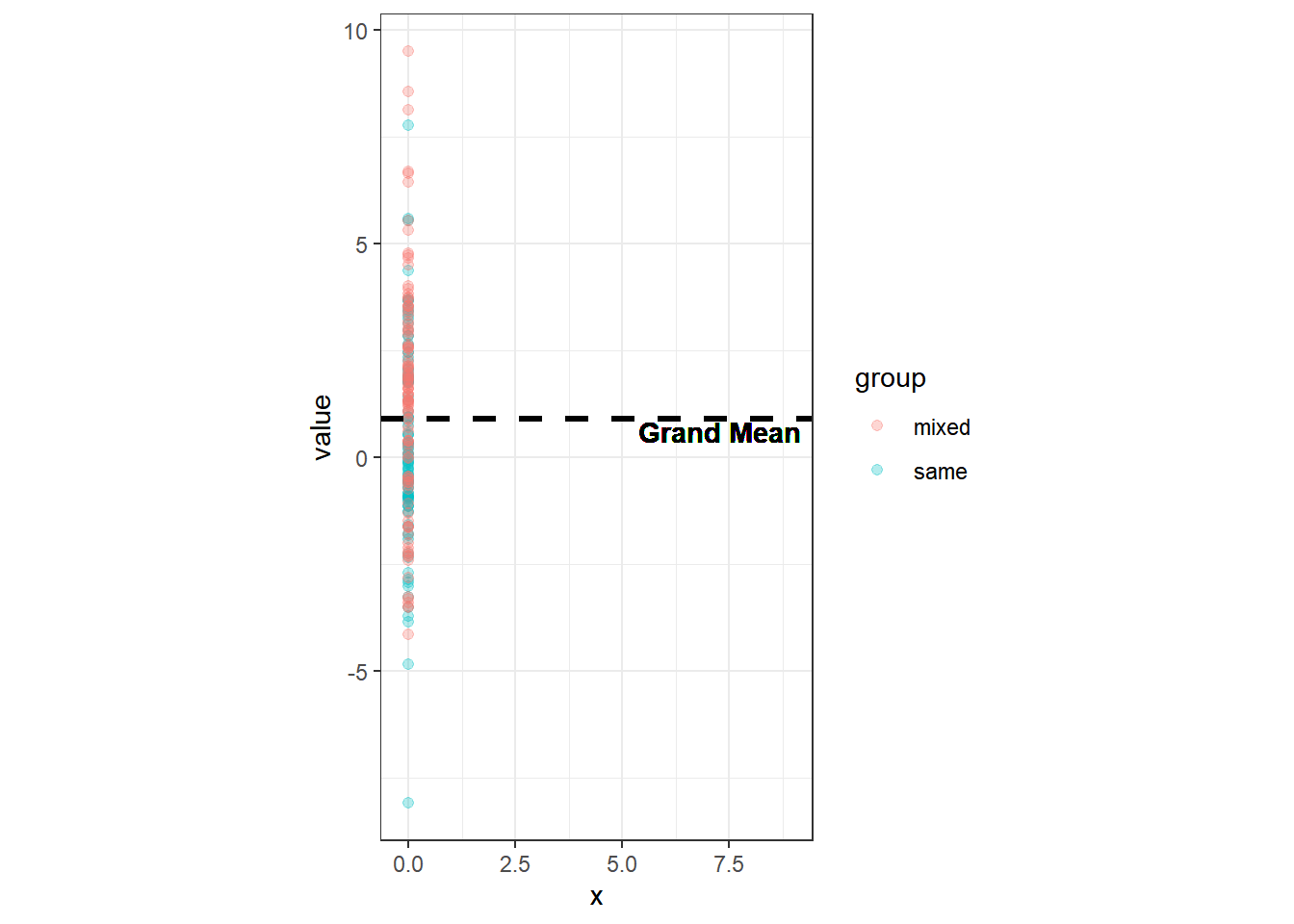
We can plot the data from both groups on the same line and calculate the mean of all values together, the so called Grand Mean. That would be the mean across all groups. The total variation of the values is the deviation of all values from this Grand Mean. This total variation can be decomposed into systematic variation — how values vary systematically between the groups — as well as into unsystematic variation — how values vary randomly within a group (i.e. error variance).
The variance for the population is defined as:
ggplot(df, aes(x=0, y=value, col=group))+
geom_rect( aes(ymin=grandmean, ymax =value, xmin = 0, xmax=0+abs(diff)),
color="black",fill="darkgray", alpha=.2) +
geom_point(alpha=.3, pos=pd, size=1.7)+
geom_hline(size=1.1, aes(yintercept=grandmean), linetype="dashed")+
theme_bw()+
coord_fixed() 
The area of all those squares would be the total Sum of Squares as a measure for the total variation. Let’s now add the systematic variation. First we need to calculate the mean of every group. The systematic variation is the difference from these means to the Grand Mean (multiplied by group size). We can visualize this systematic variation in a similar way:
ggplot(df, aes(x=0, y=value, col=group, fill=group))+
geom_rect( aes(ymin=grandmean, ymax =value, xmin = 0, xmax=0+abs(diff)), color="black", fill="darkgray",alpha=.2) +
geom_hline(size=1.1, aes(yintercept=grandmean), linetype="dashed")+
geom_point(alpha=.3, pos=pd, size=1.7)+
theme_bw()+
coord_fixed()+
geom_rect(aes(ymin=grandmean, ymax=groupmean, xmin=0, xmax=0+abs(grandmean-groupmean)), color="black",alpha=.06) +
geom_segment(aes(y=groupmean, yend=groupmean, x=0, xend=5), size=1.4, linetype="longdash" )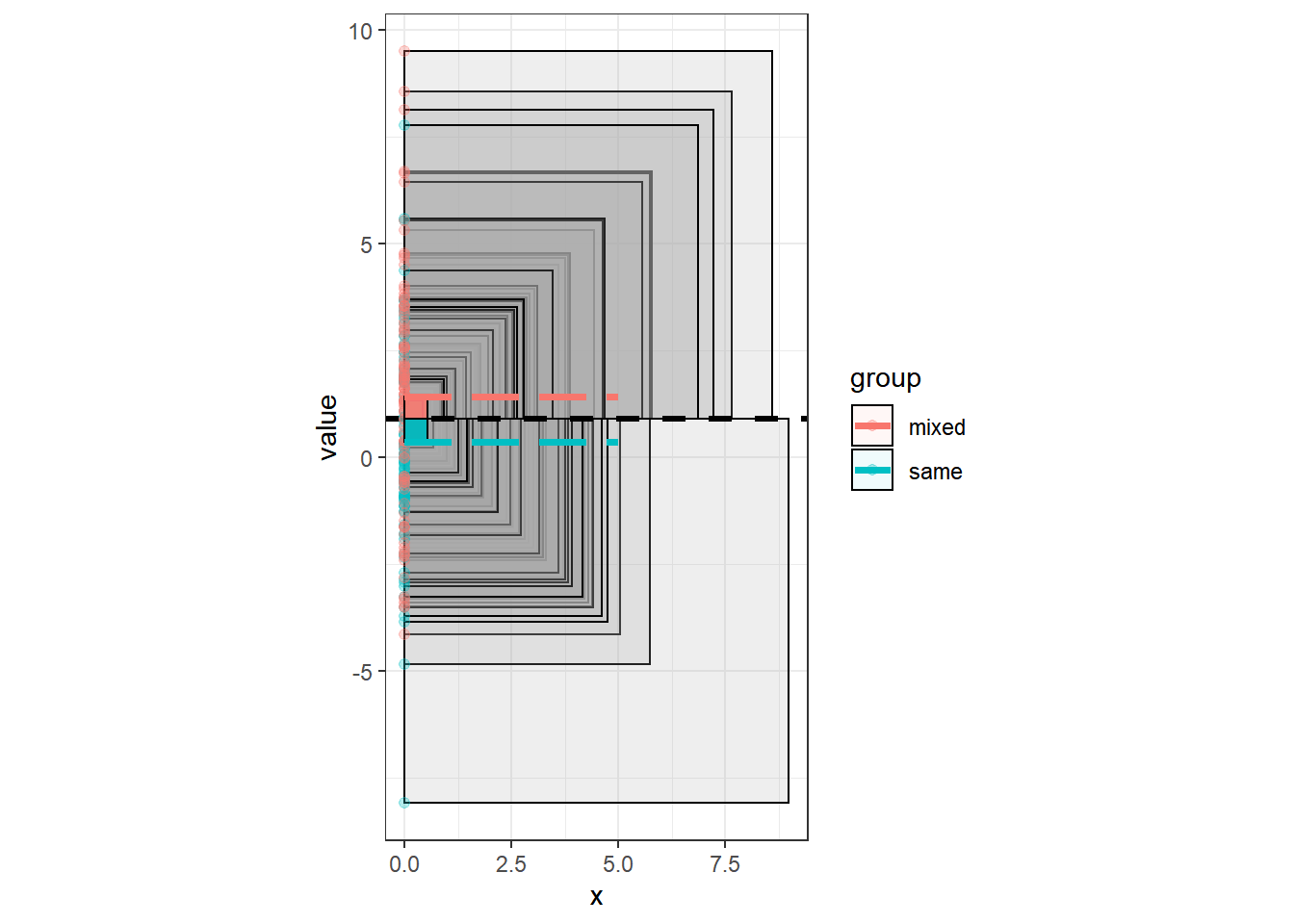
At this moment, there is a lot of overlap of the squares, and also the multiplication of the systematic variation (SS_between) with the group size is not visible. Thus, we will now add up all the squares and plot them beside each other.
Altough there is a lot of overlap on the boxes, and we have to imagine that the systematic variation gets multiplied by group size, we see already, that the area of systematic variation is much smaller than the area of the total variation. This can also be achieved mathematically and would lead us to the following ratio of between variance to total variance:
areas <- df %>%
ungroup() %>%
mutate(diff_2 = diff^2) %>%
summarise(area=sum(diff_2)) # total variation
total <- sum(df$diff^2)
# SS between is the squared difference of groupmeans to grandmean multiplied by group size
grandmean <- unique(df$grandmean)
between <- ( (mean(mixed)-grandmean)^2 + (mean(same)-grandmean)^2 ) * n
between/total## [1] 0.04372711Which leads us again exactly to our calculated
ggplot( ) +
theme_bw()+
coord_fixed()+
geom_rect(aes(xmin=0, xmax=sqrt(total),ymin=0, ymax=sqrt(total)), color="darkgray", alpha=.2)+
geom_rect(aes(xmin=0, xmax=sqrt(between), ymin=0, ymax=sqrt(between)),fill ="skyblue",alpha=.6)+
geom_text(aes(x=3.8,y=4), label="explained variance", size=3.2, col="darkblue", fontface="bold") +
geom_text(aes(x=18, y=19), label="unexplained variance",size=7.8, col="#999999", fontface="bold")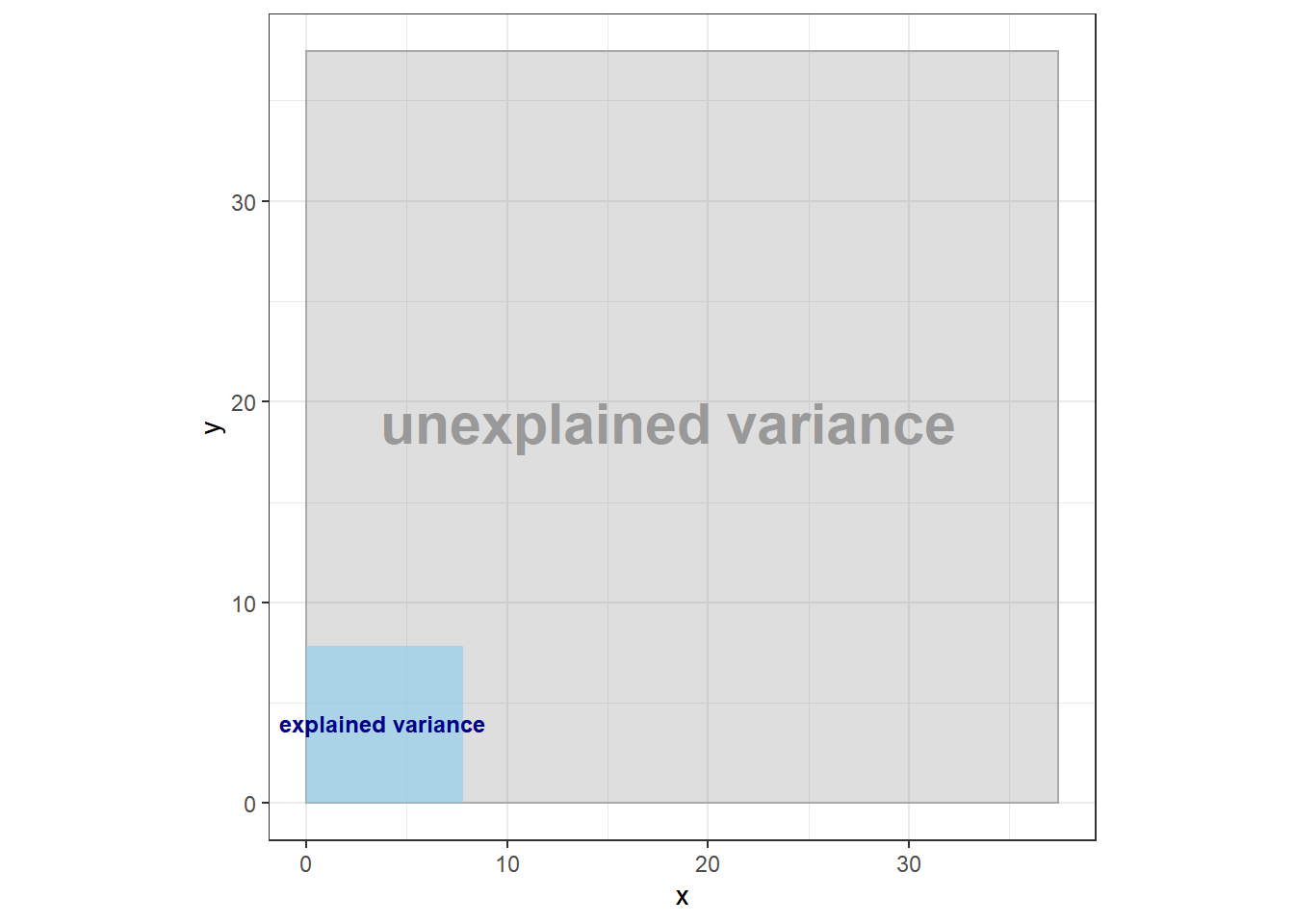
So what on earth does eta squared tell us?
We have now visualized
final_df <- data.frame(d=numeric(25000), n=numeric(25000), i=numeric(25000), Fval=numeric(25000), sign=numeric(25000), eta=numeric(25000), cohen=numeric(25000))
count <- 1
for(d in c(0,.1,.3,.5,1)){ # vary mean difference (cohen's d)
for(n in c(30,50,100,250,500)){ # vary sample size of both experimental groups
for( i in 1:1000){ # 1000 times
KG <- rnorm(n, mean=0, sd=1) #simulate sample from a standard normal distribution
EG <- rnorm(n, mean=0+d, sd=1)
temp_df <-data.frame(group=c(rep("KG",n),rep("EG",n)), value=c(KG, EG))
mod2 <- aov(temp_df$value ~ temp_df$group)
Fval <- unlist(summary(mod2))["F value1"]
sign <- unlist(summary(mod2))["Pr(>F)1"]
eta <- etaSquared(mod2)[1]
cohen <- CohenD(EG,KG)[1]
final_df[count,] <- c(d,n,i,Fval, sign, eta, cohen)
count <- count+1
}}}
#extract the following: d, n, i, F, significance, eta, cohenDggplot(final_df, aes(x=cohen, y=eta, color=Fval))+
#geom_jitter(width=.01)+
geom_point(alpha=.2)+
facet_wrap(~n)+
scale_color_viridis_c(name="F value")+
ylab("eta squared")+
#ylim(-1,2)+ coord_fixed()+
#facet_wrap(~n, scales="free_x")+ #
theme_bw()
# ggplot(final_df, aes(x=Fval, y=eta))+
# geom_point()+
# geom_smooth()+
# facet_wrap(~n)+ #very interesting!
# theme_bw() # non-linear relation?
#
# ggplot(final_df, aes(x=n, y=eta))+
# geom_point() #interestingWe can see a strong relationship between Cohen’s d and
tb <- final_df %>%
dplyr::group_by(d,n) %>%
dplyr::summarise(mean=mean(eta)) %>%
mutate(mean=round(mean,3)) %>%
spread( n, mean)
tb %>%
kable() %>%
kable_styling(bootstrap_options = "striped") %>%
column_spec(1, bold = T, border_right = T) %>%
add_header_above(c("Cohen's d", "Sample size (N)" = 5))| d | 30 | 50 | 100 | 250 | 500 |
|---|---|---|---|---|---|
| 0.0 | 0.016 | 0.010 | 0.005 | 0.002 | 0.001 |
| 0.1 | 0.018 | 0.013 | 0.008 | 0.004 | 0.004 |
| 0.3 | 0.037 | 0.033 | 0.028 | 0.024 | 0.023 |
| 0.5 | 0.076 | 0.071 | 0.064 | 0.060 | 0.060 |
| 1.0 | 0.215 | 0.210 | 0.204 | 0.202 | 0.200 |
Interestingly, the mean and upper bound of
When there is no true effect,
So far, we have now investigated how Cohen’s d and
Where do the margins .01 = small, .06 = medium, .14 = large come from?
Probably you have read or heard about such rules of thumb that an
Cohen often used standard deviations to examine effect sizes, and for ANOVAs he created a measure called
There is a dispute about the interpretation of effect sizes using the rules of thumb for small, medium, and large effects — a distinction that Correll, Mellinger, McClelland and Judd (2020) coined the “t-shirt approach”, as these categories suggest to be distinct standards to categorize effects.
On the one hand, researchers state that nothing is wrong with using such rules of thumb as benchmarks, especially, when an effect has not been studied much in literature. Also, some older reviews (Cooper, & Findley, 1982; Haase, Waechter, & Solomon, 1982; in Richardson, 2011) found that Cohen’s benchmarks on the explained variance do quite a good job, at least in social psychology and counselling psychology. They reviewed studies and found average values of the effect size lying around the values that were suggested by Cohen.
On the other hand, newer reviews suggest that the median effect sizes for example in experimental cognitive psychology might even be higher than what Cohen suggested (Schäfer & Schwarz, 2019). Furthermore, Cohen’s rules of thumb are inconsistent across different effect size measures (such as Cohen’s d,
Other estimates for the explained variance in ANOVAs
As Daniel Lakens nicely summarized here,
However, whereas sjstats package (Lüdecke, 2019) via the functions omega_sq() and epsilon_sq(). As of now,
Concluding remarks
We have now investigated the behavior of
As Richardson (2011) pointed out — despite its wide use — the interpretation of
References
- Cohen, J. (1969). Statistical power analysis for the behavioural sciences. New York: Academic Press.
- Correll, J., Mellinger, C., McClelland, G. H., & Judd, C. M. (2020). Avoid Cohen’s ‘Small’,‘Medium’, and ‘Large’for Power Analysis. Trends in Cognitive Sciences.
- Hays, W. L. (1963). Statistics. New York: Holt, Rinehart, & Winston.
- Huguet, P., & Regner, I. (2007). Stereotype threat among schoolgirls in quasi-ordinary classroom circumstances. Journal of educational psychology, 99(3), 545.
- Kelley, T. L. (1935). An unbiased correlation ratio measure. Proceedings of the National Academy of Sciences, 21, 554–559. - Leonhart, R. (2009). Lehrbuch Statistik–Einstieg und Vertiefung (2., überarbeitete und erweiterte Aufl.). Bern: Verlag Hans Huber, 92.
- Lüdecke, M. D. (2019). Package ‘sjstats’.
- Olejnik, S., & Algina, J. (2003). Generalized eta and omega squared statistics: Measures of effect size for some common research designs. Psychological Methods, 8, 434–447.
- Schäfer, T., & Schwarz, M.A. (2019). The meaningfulness of effect sizes in psychological research: differences between sub-disciplines and the impact of potential biases. Frontiers in Psychology, 10, 1-13.
- Richardson, J. T. (2011). Eta squared and partial eta squared as measures of effect size in educational research. Educational Research Review, 6(2), 135-147.